Про особливості використання моделі поведінки матеріалу у конструкціях з комірково-каркасною структурою

Вступ

Сучасний розвиток комп’ютерного моделювання глибоко інтегрувався в процеси проектування конструкцій, в тому числі в аерокосмічному сегменті. Інтенсивне залучення цифрових технологій до виробничих процесів забезпечило можливість створення адитивних технологій. Саме ці технології допомагають змінити класичні підходи до створення об’єктів та отримати високоефективні раціональні конструкції. До таких конструкцій можна віднести комірково-каркасні структури (Lattice Structure). Такі структури створюються за допомогою селективного лазерного плавлення металів (Selective Laser Melting, SLM).

Комірково-каркасні структури — є комплексними тривимірними конструкціями, які складаються з повторюваних елементів або клітин, що утворюють просторовий масив. Елементарна клітинка, що входить до структури, може мати різну геометричну конфігурацію і певною мірою представляє собою мікроферму. Саме геометрія елементарної клітинки визначає фізичні властивості структури (густину, міцність, жорсткість, анізотропію та ін.). Отже, можна підібрати геометрію таким чином, щоб забезпечити високі показники жорсткості та міцності, при цьому значно знизивши масу конструкції, що є критично важливим в аерокосмічній індустрії. Але адитивна технологія виготовлення також впливає на фізичну модель поведінки такої конструкції. Після виготовлення комірково-каркасна структура має концентратори напружень і зони локальних зв’язаних нерозплавлених частинок. Всі ці фактори впливають на фізико-механічні характеристики та властивості структури.

Слід зазначити, що комірково-каркасні структури характеризуються складною геометрією просторових масивів, тому 3D моделювання, обробка, а також числові аналізи та експерименти методами кінцевих елементів (МКЕ) вимагають надзвичайно великих ресурсів.

Мета та задачі

Дослідження побудовано на чисельному моделюванні комірково-каркасної структури. Конструкційний матеріал описується пружно-пластичною білінійною моделлю деформування.  В якості зразку розглянуто область розміром 3x3x3 елементарних комірки. Для цього зразка проведено чисельний експеримент на базі МКЕ та визначено основні фізико-механічні властивості, що матиме структурований матеріал з такою конфігурацією.

Отримані дані порівнюються з експериментальними даними, які приведені в роботі [1]. Зроблено висновки про можливість отримання фізико-механічних властивостей структурованого матеріалу для подальшого використання цих даних в процесах проектування. Теоретично, це має потенціал для уникнення необхідності точного відтворення геометрії комірково-каркасних структур та значно спростить процеси чисельних аналізів при проектуванні.

Отже, можна сформулювати наступне:

Об’єкт дослідження: конструкції з комірково-каркасною структурою, які виготовлені за допомогою адитивних технологій.

Предмет дослідження: Математичне моделювання поведінки конструкції з властивостями комірково-каркасної структури за допомогою МКЕ.

Мета дослідження: Перевірити адекватність отриманих чисельних результатів з експериментальними;  перевірити припущення про можливість скоротити необхідні обчислювальні ресурси та час для проведення розрахунків на базі МКЕ. Оцінку результату для досліджуваного зразка виконано на базі порівняння з результатами, отриманими у роботі [1]. Досліджуваний зразок має ідентичну геометрію та фізичні властивості матеріалу, що описані у вказаній роботі.

Задачі дослідження:

1. Створити 3D модель області комірково-каркасної структури розміром 3x3x3 елементарних комірки;
2. Задати властивості конструкційного матеріалу;
3. Підготувати ітераційний нелінійний аналіз стиснення даного екземпляру на базі МКЕ;
4. За результатами проведеного числового аналізу отримати дані по навантаженні, що виникає у зоні контакту при стисненні;
5. За даними геометрії та отриманих значень навантаження ви-значити показники напруження, модуля пружності і т. д.
6. Порівняти отримані результати з експериментальними результатами роботи [1] та зробити висновок.

Матеріали та методи

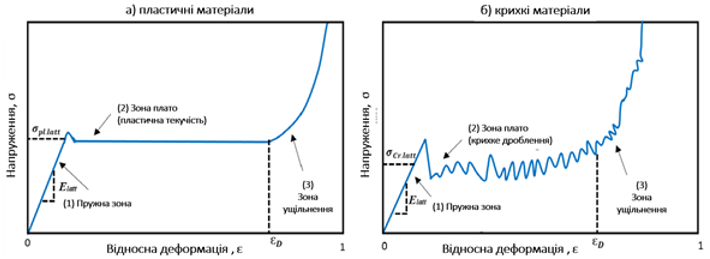
В роботі [1] автори визначають механічні характеристики створеної структури за допомогою експерименту. Матеріалу у роботі [1] задано білінійно на основі параметрів, відповідно до дослідження [3]. Згідно дослідження [2], загальну діаграму напружено-деформованого стану структурованого матеріалу можна представити у вигляді трьох зон: пружна зона, зона плато та зона ущільнення (див. рис. 1).

Рисунок 1 – Типова діаграма напружено-деформованого стану комірково-каркасної структури при стисненні: а) для пластичних матеріалів; б) для крихких матеріалів

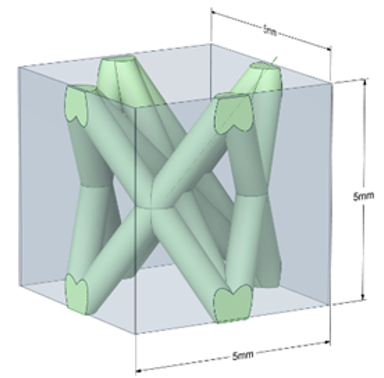
Описану модель поводження матеріалу використано у даній роботі при проведенні чисельного аналізу на базі МКЕ. Геометрія елементарної комірки для дослідження продемонстрована на Рисунку 2.

В якості конструкційного матеріалу обрано алюмінієво-кремнієвий сплав AlSi-12, що знайшов широке використання при виготовленні металевих конструкцій адитивними технологіями. Фізико-механічні властивості матеріалу вказані в Таблиці 1 [1].

Таблиця 1 – Фізико-механічні властивості AlSi-12

Рисунок 2 – Геометрія елементарної комірки

Далі створюємо модель області комірково-каркасної структури, яку будемо використовувати в числовому аналізі на базі МКЕ. 3D модель даної комірково-каркасної структури продемонстровано на рисунку 3.

Рисунок 3 – Геометрія області комірково-каркасної структури

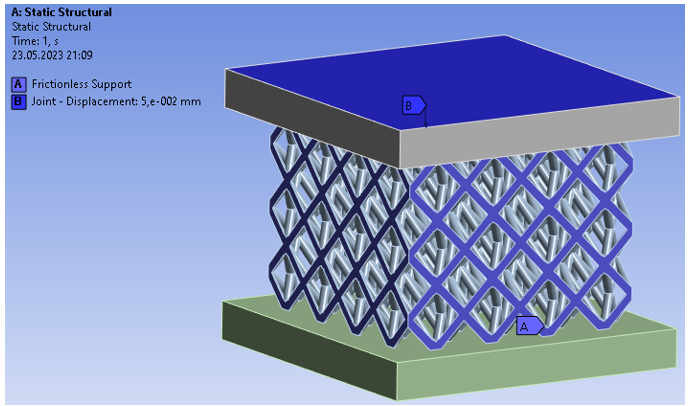
Числовий аналіз виконано за допомогою пакету кінечно-елементного аналізу ANSYS [4]. Розрахункова схема даного аналізу представлена на Рисунку 4. На схемі верхня та нижня плити є абсолютно твердими та жорсткими тілами, що не деформуються. Верхня плита ітераційно зміщується вниз, тим самим провокуючи деформації та напруження стиснення в зразку, що досліджується. При цьому в розрахунок додано умови симетрії для покращення точності результатів і їх відповідності, оскільки дана область розглядається як частина структури, а не її кінцева визначена форма.

Рисунок 4 – Розрахункова схема аналізу

Слід зазначити, що даний аналіз проводимо з допуском на високі показники деформацій для того, щоб задача проходила в пластичній зоні. Це дає змогу реалізувати закладену модель поведінки структурованого матеріалу, запропоновану в роботі [1] і показану на
Рисунку 1.

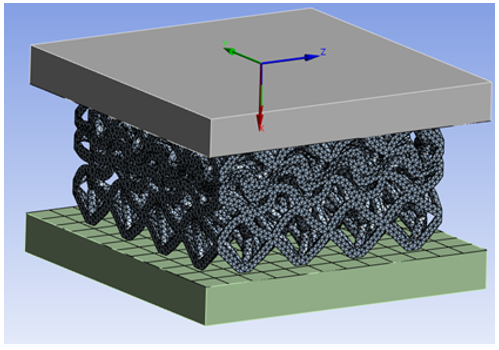
Розмір елементу сітки на комірково-каркасній структурі складає 0,5 мм. В налаштуваннях для створення кінечно-елементної сітки, обрано методи генерування сітки, що адаптовані під фізику механічного нелінійного аналізу. Порядок елементів – квадратичний. В результаті генерування сітки отримано кінечно-елементну модель досліджуваного зразка (див. на Рис. 5). Кількість вузлів – 217351, елементів – 103776.

Рисунок 5 – Кінечно-елементна модель

Даний чисельний аналіз процесу стиснення зразка проводиться ітераційно. Загалом визначено 100 ітерацій, кожен крок ітерації розбивається на підкроки в межах (10 ÷ 20) залежно від показників збіжності результату.

Загальне зміщення стискаючої абсолютно твердої та жорсткої плити складає 5 мм, що відповідає 0,33 мм/мм відносної деформації зразка. За кожен крок ітерації зміщення плити складає 0,05 мм; загальне зміщення — 5 мм.

В такій постановці задачі реалізується плавність накопичення пластичних деформацій решітчастої структури та виконуються умови квазі-статичного аналізу.

Результати

Результати чисельного моделювання проведеного аналізу по-казано на Рисунку 6.

Рисунок 6 – Результат проведеного аналізу

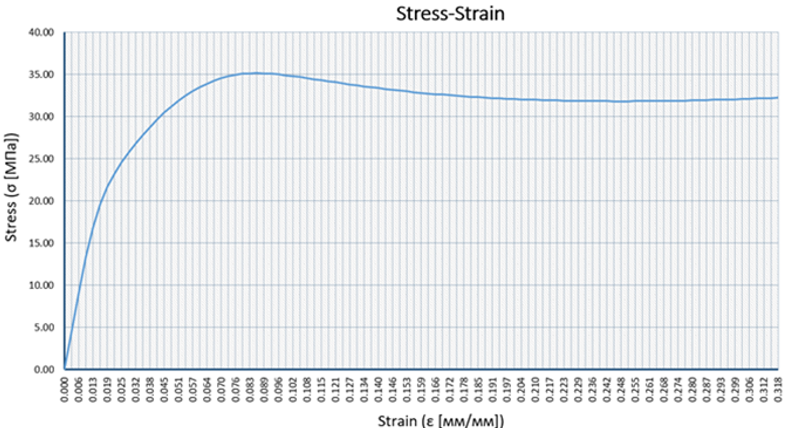
Результатом проведеного чисельного аналізу є значення стискаючого зусилля, що виникає в зоні контакту верхньої стискаючої плити з областю комірково-каркасної структури. Отримані дані інтерпретовані до значень напружено-деформованого стану та показані у вигляді графіку в координатах напруження-деформації на Рисунку 7.

Отримані результати дозволяють визначити основні фізико-механічні характеристики структурованого матеріалу та порівняти отримані значення з експерименту, що представлені в роботі [1].

Основні параметри:

• Пружна зона: пружну зону згідно з ДСТУ 2825-94 визнаємо за значенням 0,002% довжини зразка. Таким чином, межа пружності складає — σ_п=17 МПа.
• Модуль Юнга: Модуль Юнга визначаємо на пружній ділянці, консервативно — Е=1,25 ГПа.
• Умовна зона плато: Значення напружень на умовній ділянці плато становить — σ_плато=32 МПа.
• Умовна зона текучості: На діаграмі немає чітко вираженої зони початку текучості матеріалу, тому доцільно її визначати мето-дикою, прийнятою для визначення напружень при 0,2% залишкових пластичних деформацій в тілі σ_тек=18,5 МПа.
• Пікове значення напруження до зони ущільнення: відповідно до діаграми напружено-деформованого стану значення пікового напруження становить — σ_пік=35 МПа. Цей показник можна прирівняти до допустимої межі напруження для задач, в яких аналіз конструкції проходить до руйнування.

Рисунок 7 – Діаграма напружено-деформованого стану для комірково-карсної структури визначеної аналізом на основі МКЕ

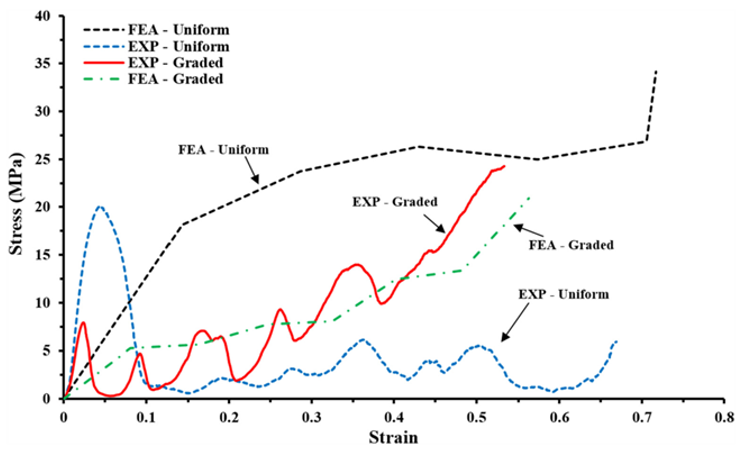
Усі визначені характерні параметри структурованого матеріалу порівняємо із даними практичного та чисельного експериментів, що отримані в роботі [1]. Результати, на основі яких проводиться порівняння показано на Рисунку 8. Дана діаграма містить інформацію про структуру 2-х різних конфігурацій решітчастої структури. Uniform — має постійну товщину мікрострижнів комірково каркасної структури, Graded — товщини мікрострижнів збільшуються по висоті досліджуваного зразка від слою до слою. Відповідно для кожної мікроструктури виконувався практичний експеримент (EXP) та чисельний аналіз (FEA).

Рисунок 8 – Діаграма напружено-деформованого стану для комірково-каркасної структури, що представлені в [1]

Порівняння результатів обох досліджень приведено в Таблиці 2.

Таблиця 2 – Порівняння результатів досліджень

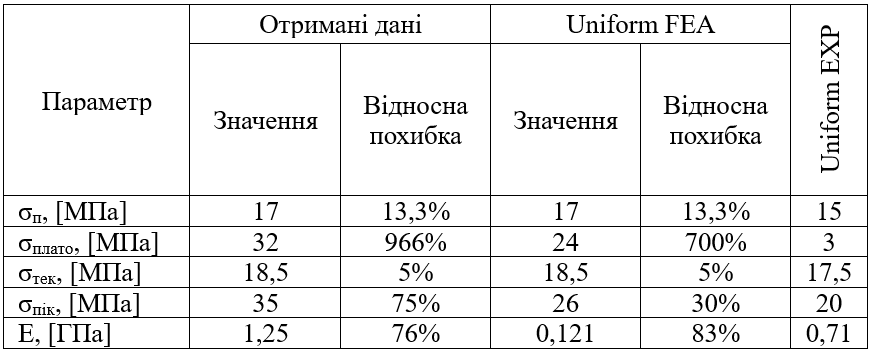
Проаналізувавши отримані результати та порівнявши їх з да-ними, що наводять автори роботи [1], видно, що результати чисельного аналізу в пружній постановці задачі та пластичній постановці задачі не дають задовільного результату для процесу деформації за пружною зоною. З результатів видно, що використання пружно-пластичного білінійного моделювання матеріалу не дозволяє виконувати квазі-статичні симуляції для визначення параметрів структурованого матеріалу. Така модель матеріалу не враховує початок руйнування мікроструктур в точках високих концентраторів напружень, втім показники напружень до початку пластичних деформацій дають невисоку похибку. Також слід зазначити, що модулі Юнга при абсолютно пластичній постановці задачі є значно вищими ніж при пружній постановці, однак обидві ці моделі дають велику погрішність у визначенні пружних властивостей структурованого металу.

Отже, розрахунково-експериментальна перевірка показала, що для комірково-каркасних структур не доцільно використовувати гетерогенну модель поведінки матеріалу, що визначається параметрами типової діаграми (див. Рисунок 1). Модель запропонована в роботі [3] не дає правдивої симуляції фізичних процесів в чисельних аналізах для отримання адекватної картини напружено-деформованого стану.

Висновки

В роботі було проведено моделювання квазі-статичного експерименту для комірково-каркасної структури з ціллю визначити фізико-механічні властивості структурованого матеріалу методами чисельного аналізу та порівняти результати з експериментальними даними роботи [1]. Задача вирішувалась в пружно-пластичній постановці з білінійним моделюванням властивостей конструкційного матеріалу з якого друкувалась 3D структура.

За результатами проведеної роботи можна зробити наступні висновки:

1. Визначення властивостей структурованого матеріалу за допомогою проведення чисельного експерименту дає задовільні результати напружень в пружній зоні, однак показники модуля пружності матеріалу мають дуже високу похибку;
2. Пікові значення напружень та значення напружень в умовній зоні плато при симуляції є значно вищими через ідеалізацію моделі та відсутність врахування процесів руйнування мікроструктури;
3. Розглянутий підхід і постановка задачі не підходить для ви-значення властивостей матеріалу. Для покращення результатів числового аналізу з ціллю визначення фізико-механічних властивостей доцільно розглядати інші методи моделювання матеріалу.
4. Гіпотеза заміни комірково-каркасної структури гетерогенною моделюю не має розрахунково-експериментального підтвердження і не може бути використана в розрахунках таких конструкцій.
5. Адитивна технологія виготовлення комірково-каркасної структури є одним з факторів який впливає на фізичну модель поведінки матеріалу. Геометрія структури комірки визначає шорсткість, яку забезпечує адитивна технологія. Це в свою чергу визначає розподіл концентраторів напружень у структурі і взагалі модель поведінки матеріалу.

Отже, дана робота наглядно демонструє, що комірково-каркасні структури залишаються досить складними для аналізів числовими методами і потребують методів, що значно спрощують вирішення даних задач. Розглянутий в представленій роботі чисельний експеримент в пружно-пластичній постановці не дає бажаного результату, однак дає розуміння процесу.

Для вирішення задачі пошуку фізико-механічних властивостей структурованого матеріалу доцільно розглянути інші методи математичного моделювання матеріалів та урахувати вплив адитивної технології. Наприклад, для вирішення даної задачі можна розглядати модель міцності Джосона-Кука [5], яка враховую зміцнення матеріалу при рості деформацій та виникнення процесів руйнування у матеріалі. Слід також зазначити, що параметри, які використовуються у згаданій моделі наявні не для всіх матеріалів і потребують проведення спеціальних практичних експериментів, що значно ускладнює проведення даних досліджень.

Посилання

1. Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM / D. S. J. Al-Saedi et al. Materials & Design. 2018. Vol. 144. P. 32–44. URL: https://doi.org/10.1016/j.matdes.2018.01.059 (date of access: 20.03.2023).
2. Mechanical Properties of the 2D Re-entrant Honeycomb Made via Direct Metal Printing / A. Alomarah et al. IOP Conference Series: Materials Science and Engineering. 2017. Vol. 229. P. 012038. URL: https://doi.org/10.1088/1757-899x/229/1/012038 (date of access: 22.03.2023).
3. Gibson L. J., Ashby M. F. Cellular Solids: Structure and Properties. 2nd ed. Cambridge : Cambridge Solid State Science Series, 1997. 510 p. URL: https://doi.org/10.1017/CBO9781139878326 (date of access: 01.04.2023).
4. Guide to ANSYS Programmable Features, ANSYS Inc., Can-onsburg, PA, January, 2018.
5. Bergström J. Plasticity Models. Mechanics of Solid Polymers. 2015. P. 353–369. URL: https://doi.org/10.1016/b978-0-323-31150-2.00007-8 (date of access: 26.03.2023).

---

---