Комп’ютерно-інтегрована технологія контролю експериментальних вимірювань з невідомими статистичними закономірностями

Сучасне виробництво неможливе без виконання розрахунків при проектуванні і перевірці якості готових деталей і їх частин у відповідності до технічних вимог. Всі вихідні для розрахунків числа, за рідкісними виключеннями, є продуктами вимірювань. У властивостях експериментальних вибірок міститься інформація не лише про об’єкт, а також і про вимірювальні процедури. В процесі контролю якості продукції ключову роль відіграє коректна та адаптивна технологія обробки вимірювань.

В роботі розглянута задача еталонної дефектоскопії, яка використовує лише еталони норми, а еталонів браку для виявлення дефектів або відхилень в технічних об’єктах не має [1]. Передбачається, що в результаті контролю отримано вибірки вимірювань, що характеризують нормальний стан об’єкту. Отже, всі інші стани, які відрізняються від нормального, будуть вважатися дефектними або ненормальними. Для вирішення задач такого типу можна застосовувати статистичні критерії однорідності. Серед критеріїв перевірки однорідності вибірок випадкових величин розрізняють параметричні та непараметричні критерії [2-4]. Параметричні критерії можуть бути застосовані тільки до даних, що мають певні припущення про певний закон розподілу ймовірностей. Тобто, вони застосовуються тільки для певних законів і невідомість зберігається на рівні параметрів [5]. Непараметричні критерії – це критерії, які не потребують знань параметрів розподілу вибірки та не залежать від конкретного виду закону розподілу ймовірностей. Більшість непараметричних критеріїв є ранговими, а саме ґрунтуються на ранжуванні даних, тобто перетворенні вхідних даних на послідовність за їхньою величиною, а потім на порівнянні цієї послідовності з іншими послідовностями даних. Ці критерії можуть бути використані для порівняння середніх значень, медіан, дисперсій і інших характеристик двох або більше вибірок [5].

Застосування рангових критеріїв дозволяє здійснювати контроль стану технічних об’єктів без потреби знань про статистичні закономірності вимірювань. Існують непараметричні критерії, які перевірять гіпотезу про однорідність вибірок окремо за зсувом та окремо за масштабом [2].

Метою роботи є розробка комп’ютерно-інтегрованої технології, яка призначена для автоматизації прийняття рішень щодо стану об’єктів в задачах еталонної дефектоскопії. Для автоматизація прийняття рішень потрібно обрати такі критерії, які є ефективними в умовах обмеженості і невизначеності вхідних даних. В якості непараметричного критерія зсуву в роботі запропоновано потужний та відомий критерій Манна-Уітні-Вілкоксона, а в якості критерія масштабу – критерій Клотца.

Для досягнення сформульованої мети необхідно вирішити такі задачі, як розробка алгоритмів для реалізації критеріів Манна-Уітні-Вілкоксона та Клотца. На основі розроблених алгоритмів необхідно сформувати блок-схему комп’ютерно-інтегрованої технології для одночасного контролю зсуву і масштабу.

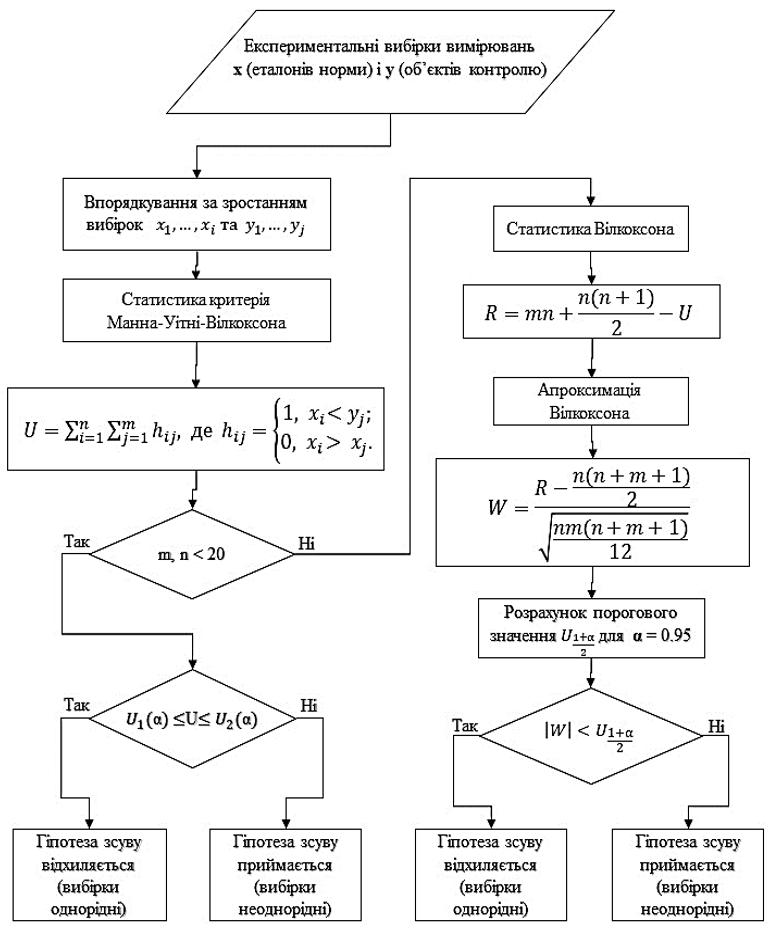
Основна ідея критерію Манна-Уітні-Вілкоксона [6, 8] полягає на порівнянні між собою рангів спостережень у двох вибірках і визначенні, чи є статистично значима відмінність між ними. Цей критерій може бути застосований до даних з будь-яким законом розподілу ймовірностей, що робить його більш гнучким, ніж критерій Стьюдента, який в свою чергу, вимагає щоб дані мали нормальний закон розподілу ймовірностей.

Алгоритм критерія Манна-Уітні-Вілкоксона відбувається наступним чином:

1. Задається довжина порівнюваних вибірок та кількість цих вибірок (дослідів).
2. Генеруються експериментальні вибірки з різними коефіцієнтами асиметрії.
3. Впорядковуються за зростанням порівнювані вибірки вимірювань.
4. Розраховуються статистика критерія Манна-Уітні-Вілкоксона.
5. Якщо досліджуються вибірки з довжиною, меншою за 20, то порівнюється ця статистика U з пороговими значеннями U1(a) та U2(a), які беруться з таблиці критичних значень критерія Манна-Уітні-Вілкоксона [7]. Після цього приймається гіпотеза, щодо однорідності вибірок за зсувом.
6. Якщо досліджуються вибірки з довжино, більшою за 20, то застосовується апроксимація, яка зв’язана з статистикою Вілкоксона. Після цього, вже розрахований показник Вілкоксона порівнюється з розрахованим пороговим значенням. Якщо значення показника W менше порогового значення, то тоді приймається нулева гіпотеза, щодо одноріності вибірок за зсувом [9].

На рис. 1 показано розроблений алгоритм реалізації критерія Манна-Уітні-Вілкоксона.

Рисунок 1 – Схема алгоритму реалізації критерія Манна‑Уітні‑Вілкоксона

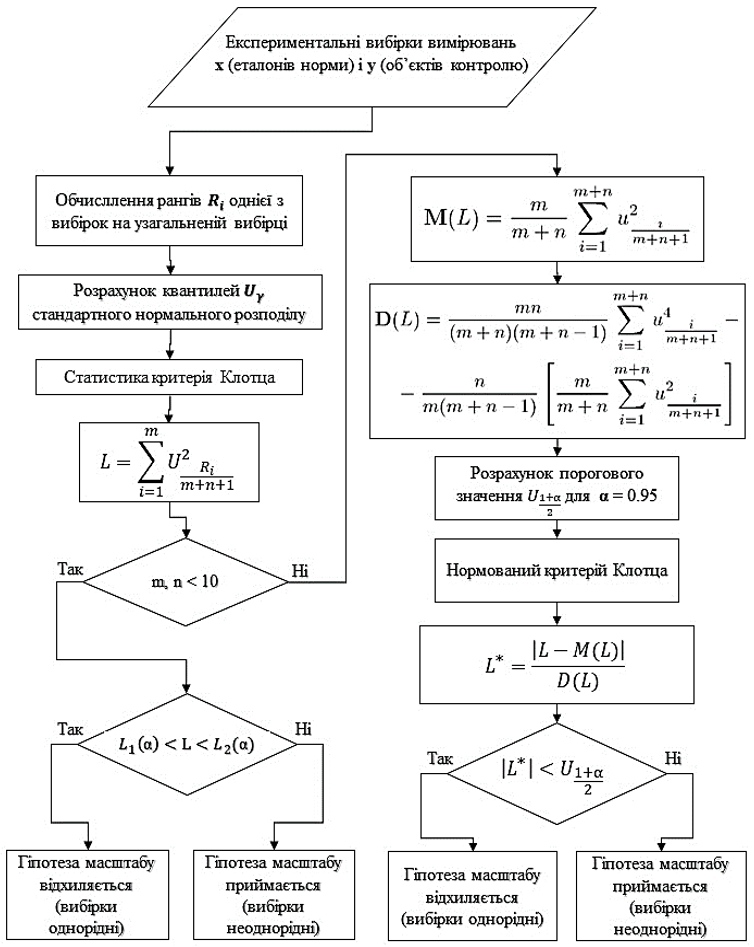
Критерій Клотца [11] є непараметричним критерієм масштабу. Тобто він базується на порівнянні дисперсій або середніх рангів в двох, трьох або більше вибірок вимірювань.

Основна ідея критерія Клотца полягає в тому, що якщо дисперсії вибірок є однаковими та не відрізняються значущим чином, то можна припустити, що ці вибірки належать до однієї генеральної сукупності.

Алгоритм критерія Клотца відбувається наступним чином:

1. Задається довжина порівнюваних вибірок та кількість цих вибірок (дослідів).
2. Генеруються експериментальні вибірки з різними коефіцієнтами асиметрії.
3. Обчислюються ранги однієї з вибірок на узагальненій вибірці.
4. Розраховуються квантилі стандартного нормального розподілу та обчислюється статистика критерія Клотца.
5. Якщо досліджуються вибірки довжиною, меншою за 10, то порівнюється ця статистика L з пороговими значеннями, які беруться з таблиці критичних значень критерія Клотца [10]. Після цього приймається гіпотеза, щодо однорідності вибірок за масштабом.
6. Якщо досліджуються вибірки довжиною, більшою за 10, то розподіл статистик L задовільно апроксимується нормальним із математичним очікуванням і дисперсією за відповідними формулами. Після цього, розраховується вже нормований критерій Клотца та порівнюється з розрахованим пороговим значенням. Якщо значення показника L менше порога, тоді приймається нулева гіпотеза, щодо одноріності вибірок за масштабом [11].

На рис. 2 продемонстровано розроблений алгоритм реалізації критерія Клотца.

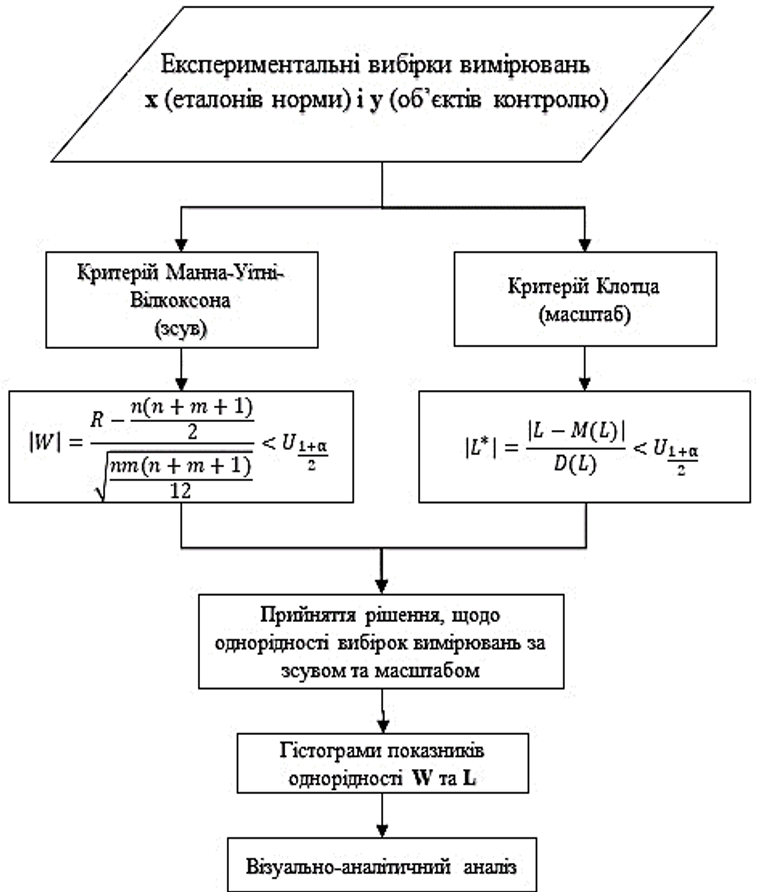
На рис. 3 показана схема комп’ютерно-інтегрованої технології контролю зсуву і масштабу. Таким чином, на вхід комп’ютерно-інтегрованої технології надходять експериментальні вибірки, які характеризують нормальний стан об’єкту контролю та вибірки контрольованого об’єкту, який знаходиться в невідомому стані. Розроблена технологія дозволяє контролювати і зсув, і масштаб. Критерій Клотца і Вілкоксона в запропонованій технології виконуються паралельно. За результатами виконання цих критеріїв приймається рішення, однорідні вони чи ні. Після прийняття рішення, щодо однорідності вибірок вимірювань, проводиться візуально-аналітичний аналіз за побудованими гістограмам показників критеріїв Манна-Уітні-Вілкоксона та Клотца.

Рисунок 2 – Схема алгоритму реалізації критерія Клотца

В результаті проведеної роботи розроблено схеми алгоритмів для реалізації критеріів Манна-Уітні-Вілкоксона та Клотца. На основі розроблених алгоритмів сформована комп’ютерно-інтегрована технологія контролю експериментальних вибірок вимірювань, яка дозволяє перевіряти їх щодо зсуву та масштабу одночасно.

Рисунок 3 – Блок-схема комп’ютерно-інтегрованої технології контролю зсуву і масштабу

Запропонована в роботі технологія контролю не залежить від виду статистичних закономірностей вибірок вимірювань, а отже вона може бути запропонована для вирішення практичних задач еталонної дефектоскопії в умовах невизначеності статистичних закономірностей експериментальних вибірок вимірювань.

Розроблену комп’ютерно-інтегровану технологію планується дослідити шляхом проведення розрахункових експериментів. Генеруючі однорідні та неоднорідні вибірки та керуючи їх статистичними властивостями, планується оцінити ефективність запропонованої технології.

У найближчій перспективі проведення обчислювальних експериментів та побудова графіків залежностей емпіричних ймовірностей розпізнавання при зсуві та зміні масштабу з метою обґрунтування практичних рекомендацій щодо застосування розробленої комп’ютерно-інтегрованої технології контролю експериментальних вимірювань з невідомими статистичними закономірностями.

Посилання

1. Малайчук В. П., Клименко С. В., Лысенко Н. А. Математическая дефектоскопия. Монография, Второе издание. – Днепр: репозиторий ДНУ имени Олеся Гончара, 2017 – 180 с. (http://repository. dnu. dp. ua:1100/?page=inner_material&id=9331)
2. Кобзарь А. И. Прикладная математическая статистика. Для инженеров и научных работников. – М. : ФИЗМАТЛИТ, 2006. – 816 с. – ISBN 5-9221-0707-0
3. Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007. – 368 с.
4. Малайчук В. П., Петренко О. М., Рожковський В. Ф. Обробка вимі-рювань і сигналів неруйнівного контролю: Навч. посіб. – Д. : РВВ ДНУ, 2004. – 144 с.
5. Бахрушин В. Є. Методи аналізу даних : навчальний посібник для студентів / В. Є. Бахрушин. – Запоріжжя : КПУ, 2011. – 268 с.
6. Mann H. B., Whitney D. R. On a test the whether one of two random variables is stochastically larger than the other // AMS. 1947. V. 18. P. 50-60.
7. Ликеш И., Ляга Й. Основные таблицы математической статистики. – М. : Финансы и статистика, 1985.
8. Руденко В. М. Математична статистика. Навч. посіб. – К. : Центр учбової літератури, 2012. – 304 с
9. Singh N. The ratio test for the parameters exponential distributions // Commun. Stat. -Theor. Meth. 1985. V. 13, №6. P. 116-119.
10. Sidak Z. Tables for two normal-scores tests for the two-sample scale problem // Aplik. Matematiky. 1973. V. 18, №5. P. 346-363.
11. Klotz J. Nonparametric tests for scale // AMS. 1962. V. 33, P. 498-512.

---

---