Чисельне дослідження фізичного механізму виникнення тонального шуму аеродинамічних профілів
Сергій Вікторович Алексєєнко
Дніпровський національний університет імені Олеся Гончара, Дніпро
Валерій Євгенович Некрасов
Дніпровський національний університет імені Олеся Гончара, Дніпро
Виникнення аеродинамічного шуму, який створюється повітряним потоком при обтіканні конструктивних елементів технічних пристроїв, є однією з актуальних інженерних проблем. У сучасному світі все більша увага приділяється питанням екології та забезпечення безпеки життєдіяльності, зокрема, зниження негативного впливу шумового забруднення. Прикладами джерел аеродинамічного шуму є дорожні транспортні засоби, швидкісний залізничний транспорт, авіаційна техніка, промислове обладнання, вітряні турбіни.
Розуміння фізичних механізмів, які полягають в основі генерації звуку, має важливе значення при розробці технологій зменшення шуму, а основним завданням стає точне моделювання аеродинамічного та акустичного полів, створюваних обтічним тілом.
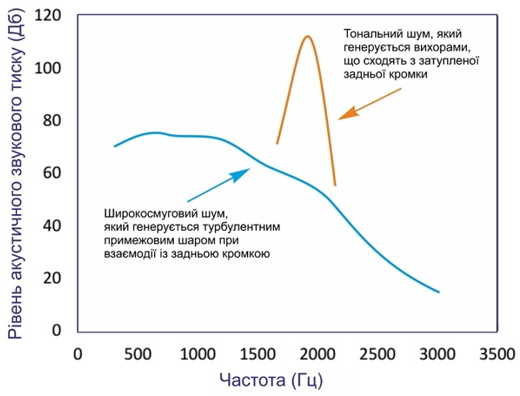
Шум, що виникає при обтіканні аеродинамічних профілів, можна класифікувати як широкосмуговий і тональний (рис. 1) [1].
Рис. 1. Шум аеродинамічного профілю
Широкосмуговий шум характеризується відносно однорідним розподілом звуку в діапазоні частот. Вважається, що для турбулентних профілів вихрові структури, що відносяться до турбулентного прикордонного шару, переміщаючись вздовж обтічної поверхні при взаємодії з задньою кромкою, розсіюються, генеруючи акустичні хвилі (створюючи широкосмуговий шум).
Тональний шум характеризується більшою інтенсивністю у вузькому діапазоні частот. Такий шум може виникати при обтіканні турбулентних профілів із затупленою задньою кромкою, що генерує відносно великі вихрові структури, а також при збільшенні кута атаки і виникненні відриву потоку, що супроводжується викидом великих вихрових структур у слід. Також тональний шум може виникати під час обтікання перехідних профілів, коли під дією негативного градієнта тиску ламінарний прикордонний шар відокремлюється, стаючи, під дією збурень, що посилюються, турбулентним. При цьому в прикордонному шарі посилюється перемішування та передача імпульсу у нормальному до стінки напрямку. В результаті, втрачаючи енергію, прикордонний шар повторно приєднується до обтічної поверхні, утворюючи так званий «пузир розділення». При цьому за областю повторного приєднання за рахунок нестійкості прикордонного шару генеруються вихори, які розвиваються, рухаючись уздовж обтічної поверхні і, в подальшому, при взаємодії з задньою кромкою профілю, генерують тональний шум, який може переважати над загальним широкосмуговим фоном, досягаючи 40 дБ.
Основна увага в даному дослідженні приділена вивченню тонального шуму, що виникає при обтіканні перехідних профілів.
Сучасний рівень розвитку комп’ютерної техніки та методів обчислювальної аерогідродинаміки відкриває можливість активного проведення аероакустичних досліджень. При цьому обчислювальні аероакустичні завдання можна вирішувати за допомогою двох основних підходів: прямого акустичного моделювання (DAS – Direct Acoustic Simulation) та гібридних методів [2].
Метод DAS дозволяє одночасно отримувати як гідродинамічні, так і акустичні величини шляхом безпосереднього розв’язання рівнянь Нав’є-Стокса для стисливих середовищ. Цей метод є природним способом розрахунку генерації звуку, оскільки основні рівняння повністю описують фізику явища. Також перевагами такого підходу є відсутність обмежень внаслідок прийнятих припущень, можливість уточнення потоко-акустичних зв’язків та можливість відстеження процесів генерації та поширення звуку у ближньому та середньому полях. Необхідно зазначити, що хоча DAS вимагає значних обчислювальних ресурсів, особливо для вирішення інженерних завдань, з розвитком технологій високопродуктивних обчислень методи прямого моделювання стають дедалі доступнішими. У цьому випадку бажаним є застосування вирішувачів з високою надійністю, сумісністю та можливістю паралельних обчислень [3].
Гібридні методи полягають у використанні двох різних чисельних вирішувачів: нестаціонарного інструменту обчислювальної гідродинаміки як генератора джерела звуку та акустичного вирішувача як методу перенесення. При цьому акустичний вирішувач може бути заснований на розв’язанні системи диференціальних рівнянь у часткових похідних, таких як лінійні рівняння Ейлера [4] або рівняння акустичних збурень [5], або як інтегральний метод, наприклад, заснований на роботі Джеймса Лайтхілла [6]. З обчислювальної точки зору інтегральні методи менш затратні, дозволяють мати явне рішення для акустичного тиску, яке має бути чисельно оцінене з вихідних умов, отриманих за допомогою розв’язання рівнянь Нав’є-Стокса, та на сьогоднішній день є більш доступними та популярними для моделювання аеродинамічного шуму.
В роботі розглянуто можливість використання пакета ANSYS Fluent для розрахунку аеродинамічних та акустичних характеристик профілів. Наведено порівняння отриманих результатів з відомими розрахунковими та експериментальними даними.
В обраній методиці щільність повітряного потоку моделюється рівнянням стану ідеального газу, тангенціальні напруги визначаються згідно з гіпотезою Стокса, в’язкість – згідно із законом Сатерленда.
Чисельна реалізація передбачає спочатку знаходження поля розподілу швидкості та тиску в розрахунковій області з подальшим обчисленням значень щільності та інших термодинамічних властивостей шляхом розв’язання рівняння енергії та рівняння стану. Прийнято зв’язану схему розв’язання рівнянь тиск-швидкість, що забезпечує більш високу швидкість збіжності, однак, при цьому має вищі вимоги до обсягу пам’яті. Чисельна просторова дискретизація реалізована із використанням методу найменших квадратів для оцінки градієнтів, схему другого порядку точності для тиску, протипоточну схему другого порядку точності для щільності, імпульсу і енергії.
При моделюванні турбулентності використовується метод великих вихорів (LES – Large Eddy Simulation) із застосуванням моделі підсіткової в’язкості Смагоринського.
В роботі досліджено структуру течії, відтворено характерні особливості, такі як утворення «відривного пузиря» та подальше послідовне виникнення вихорів, що сходять. Наведено анімовані ілюстрації результатів, що дозволяють детальніше вивчити фізичну картину процесів вихроутворення, і, відповідно, генерування звукових коливань.
Показано, що нестійкість на нижній частині профілю, яка здійснює коливальні рухи із частотою, що корелюється із частотою сходження вихорів з задньої кромки, а також нестійкість в примежовому шарі на верхній поверхні профілю (в області відривного пузиря) впливають на формування частоти зриву вихорів. Змодельована фізика процесу генерування нестійкостей та вихорових структур якісно збігається із прийнятою теорією виникнення тонального шуму.
Також отримані моментальні та усереднені за часом значення розподілу коефіцієнтів тиску та тертя вздовж обтічної поверхні профілю, визначені поздовжні координати точок відділення та повторного приєднання примежового шару.
Отримані дані щодо коливань коефіцієнта підйомної сили досліджуваного профілю (як таких, що корелюють із домінуючим тональним шумом), наведено розподіл їх частотних спектрів. Наведено картини флуктуацій тиску, що генеруються вихровими структурами які взаємодіють із задньою кромкою профілю, і поширюються в ближньому полі.
Результати роботи можуть бути використані при вивченні фізики процесів генерації звуку при обтіканні профілів повітряним потоком, а також розробці та оцінці методів зниження аеродинамічного шуму.
Посилання
- W.W. Hiner, “Numerical Investigation of Tonal Noise on a Transitional Airfoil under Varying Conditions”, 2015.
- M. Navarrete, “Computational aeroacoustics in the automotive industry,” Tesi doctoral, UPC, Departament d’Enginyeria Mecànica, 2021.
- D. Huang, Z. Yang, R. Chi Kin Leung, “Implementation of Direct Acoustic Simulation using ANSYS Fluent,” INTER-NOISE and NOISE-CON Congress and Conference Proceedings, InterNoise21, Washington, D.C., USA, pages 970-1944, pp. 1243-1252(10), 2021.
- C. Bailly, C. Bogey, “An overview of numerical methods for acoustic wave propagation,” in European Conference on Computational Fluid Dynamics, ECCOMAS CFD, P. Wesseling, E. Onate, J. Périaux (Eds), 2006.
- R. Ewert, W. Schröder, “Acoustic perturbation equations based on flow decomposition via source filtering,” Journal of Computational Physics, vol. 188, no. 2, pp. 365–398, 2003.
- M. J. Lighthill, “On sound generated aerodynamically. i. general theory,” in Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 1952, vol. 211, no. 1107. The Royal Society, 1952, pp. 564–587.