Синтез конструкторських рішень для корпусів високотискових насосів
Олег Євгенійович Бондаренко
Дніпровський національний університет імені Олеся Гончара, Дніпро
Олег Петрович Бадун
FlightControl Propulsion, Дніпро
Юрій Валентинович Ткачов
Дніпровський національний університет імені Олеся Гончара, Дніпро
Вступ
Розвиток сучасної ракетно-космічної техніки складно уявити без розвитку і впровадження нових технологій виробництва. Одним із таких нововведень і є 3D-друкування. Розвиток адитивних технологій дав змогу отримати практично необмежені за складністю геометричні форми деталей і агрегатів, що було неможливим під час використання класичних методів виготовлення та обробки. Використання нових форм і дизайну з впровадженням топологічної оптимізації допомагає більш ефективно і раціонально використовувати матеріал, а також створювати полегшені та вдосконалені конструкції, які відповідають нормам міцності, стійкості і так далі.
Топологічна оптимізація конструкцій є математичним підходом, здатним вирішити низку поставлених завдань для інженерів. Ітеративно вирішується проблема раціонального розподілу матеріалу в конструкції в обмеженому просторі, з урахуванням граничних умов і діючих навантажень. Метод топологічної оптимізації використовується на початковій стадії розроблення конструкцій або модернізації наявних. Отримане оптимальне рішення модернізується виходячи з вимог технологічності та функціоналу. Цей підхід дає змогу істотно заощадити час на початковому етапі проектування конструкції.
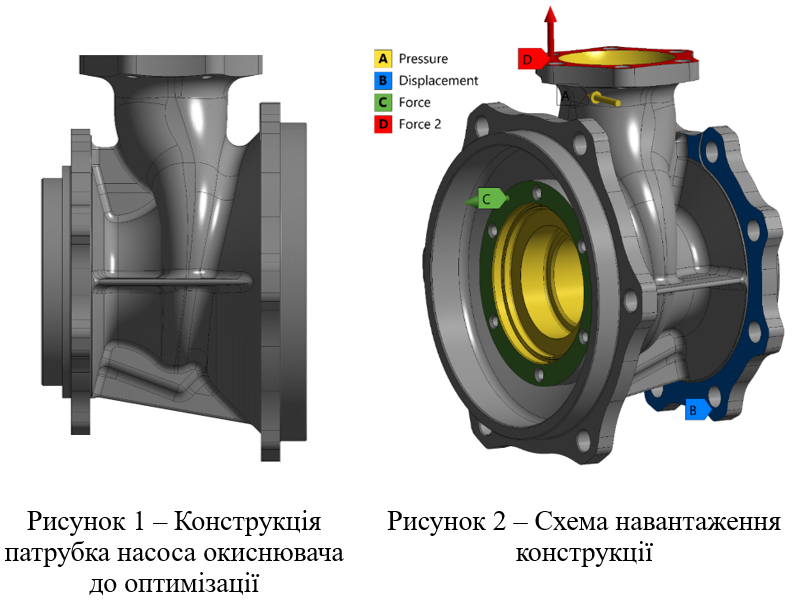
У цій роботі представлено результати впровадження технології SLM (Selective Laser Melting) [4] і топологічної оптимізації, проведеної в компанії FlightControl Propulsion [5], на прикладі реалізації конструкції патрубка насоса окиснювача турбонасосного агрегату (ТНА) рідинного ракетного двигуна (РРД) (рис. 1). Схема навантаження корпусу насоса окиснювача імітує реальний тиск, який діє на конструкцію (рис. 2).
Складність упровадження цієї технології зумовлена відсутністю статистичних даних щодо застосування SLM-технології під час виготовлення елементів конструкції РРД, зокрема, немає стандартів, що регулюють систему якості. Так само складність являє собою і те, що характеристики і якість одержуваних виробів безпосередньо залежить від безлічі чинників (самого принтера, якості порошку тощо).
Мета та задачі
Існує дві схеми подачі палива з паливних баків у двигун. Турбонасосна система подачі палива рідких компонентів ракетного палива або робочого тіла (подача окиснювача і пального здійснюється насосами, які приводяться в дію газовою турбіною). Вимоги до турбонасосних агрегатів не стоять на місці, постійно динамічно змінюючись, починаючи від матеріалів, з яких виготовлятимуть ТНА до освоєння нових компонентів палива.
Турбонасосний агрегат є одним зі складних агрегатів у ракетному двигуні. [3] За статистикою понад 54% виходу двигунів з ладу є відмова турбонасосного агрегату. Тому до такого агрегату виставлено більш жорсткі вимоги щодо надійності та міцності. Оскільки тиск у насосах може досягати сотень атмосфер, то і запас міцності має бути високим. Так само існує проблема в тому, що елементи турбонасосного агрегату мають занадто велику масу, що в умовах ракетної техніки має бути зведене до мінімуму, оскільки головним критерієм у ракетній техніці є мінімум маси.
Метою даної роботи є показати цикл отримання оптимальної конструкції за допомогою топологічної оптимізації на прикладі такого елемента конструкції РРД. Матеріал для виготовлення даної конструкції – алюмінієвий сплав для 3Д-друку. Ця проблема існує тривалий час, оскільки проектування ТНА завдання складне з погляду раціонального використання матеріалу в конструкції та підвищеної вимоги щодо міцності до цього агрегату.
Турбонасосний агрегат є важливою частиною конструкції РРД. Його сумарна маса в конструкції РН може бути досить великою, тому мінімізація маси турбонасоса в конструкції РН і зокрема РРД є важливим завданням.
Провести топологічну оптимізацію конструкції (рис. 1) і досягти таких результатів:
– мінімізувати масу патрубка насоса окиснювача ТНА;
– забезпечити достатню міцність патрубка насоса окиснювача.
Схема навантаження конструкції імітує реальний тиск у патрубку насоса окиснювача (рис. 2).
Матеріали і методи
Для опису конструкції та її подальшої зміни використовується система рівнянь механіки суцільних середовищ (рівняння руху, геометричного співвідношення і закон Гука), вони мають такий вигляд:
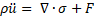
де, ∇ – оператор набла, σ – тензор напружень Коші, F – вектор зовнішніх сил на одиницю об’єму.
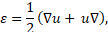
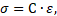
де С – тензор пружних модулів.
На рис. 2 прийнято такі позначення:
– Синім кольором позначено торець кріплення, фіксація деталі по осі Х – межа S1;
– Жовтим кольором позначені поверхні, на яких діє тиск р – межа S2;
– Зеленим кольором позначено торець, на який діє розтягувальне зусилля T1 від тиску р – межа S3;
– Червоним кольором позначено торець, на який діє розтягувальне зусилля T2 від тиску р – межа S4.
Математичні граничні умови будуть записані таким чином:
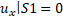
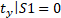
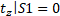
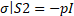
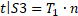
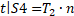
Ці граничні умови визначають напружено-деформований стан (НДС) конструкції. Так само було виставлено обмеження за масою, яке мало такий вигляд:
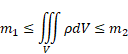
Аналітичне розв’язання системи рівнянь не є можливим через геометричну складність. Тому для розв’язання задачі використовують чисельні методи, а саме кінцево-елементні методи. Де область інтегрування поділяється на кінцеві елементи, усередині яких шукані змінні апроксимуються безперервними функціями. Даний метод гарний тим, що йде безперервна апроксимація по всьому простору, на відміну, наприклад, від методу кінцевих різниць. Суть методу полягає в його назві. Область, у якій шукається розв’язок диференціальних рівнянь, розбивається на певну кількість подібностей (елементів). У кожному з елементів довільно вибирають вид апроксимуючої функції [1].
У найпростішому випадку це поліном першого ступеня. Поза своїм елементом апроксимувальна функція дорівнює нулю. Значення функцій на межах елементів (у вузлах) є розв’язанням задачі і заздалегідь невідомі. Коефіцієнти апроксимувальних функцій зазвичай шукають з умови рівності значень сусідніх функцій на межах між елементами (у вузлах). Потім ці коефіцієнти виражаються через значення функцій у вузлах елементів. Складається система лінійних алгебраїчних рівнянь. Кількість рівнянь дорівнює кількості невідомих значень у вузлах, на яких шукають розв’язання вихідної системи, прямо пропорційна кількості елементів і обмежується тільки розрахунковими можливостями. Оскільки кожен з елементів пов’язаний з обмеженою кількістю сусідніх, система лінійних алгебраїчних рівнянь має розріджений вигляд, що істотно спрощує її розв’язання.
Якщо говорити в матричних термінах, то збираються так звані матриці жорсткості 𝐾 і мас 𝑀. Далі на ці матриці накладаються граничні умови [2] (наприклад, за умов Неймана в матрицях не змінюється нічого, а за умов Діріхле з матриць викреслюються рядки та стовпчики, відповідні граничним вузлам, тому що через крайові умови значення відповідних компонентів розв’язку відоме). Потім збирається система лінійних рівнянь і розв’язується одним із відомих методів.
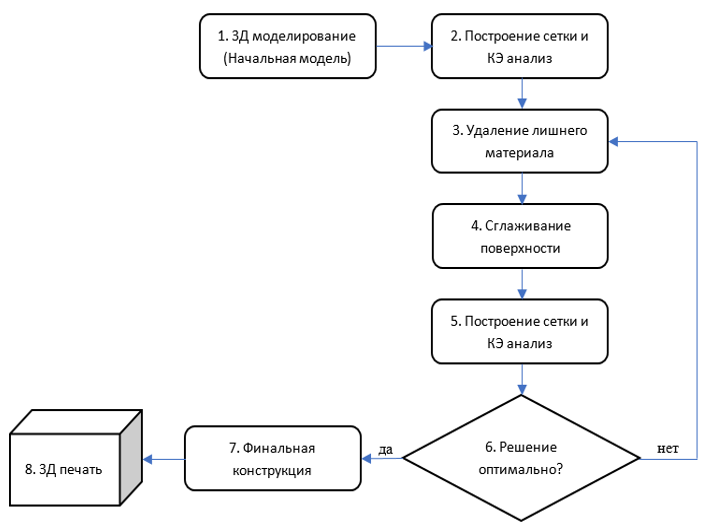
На рис. 3 представлено схему процедури конструкції за допомогою топологічної оптимізації. А також описано алгоритм дій під час оптимізації конструкції.
Рисунок 3 – Схема процедури конструкції за допомогою топологічної оптимізації
Початковим етапом є побудова початкової конструкції (пункт 1). Потім проводиться її кінцево-елементний аналіз, відповідно до схеми навантаження і граничних умов (пункт 2). Потім проводиться топологічна оптимізація конструкції (пункти 3 – 6). Початкова конструкція представляється у вигляді набору вокселів.
На цьому етапі використовують SIMP (Solid Isotropic Material with Penalization) метод, або метод пеналізації для твердого ізотропного тіла, – метод топологічної оптимізації, ідея якого полягає у створенні віртуальної густини, що представляє аналог деякої реальної характеристики об’єкта. Тобто суть методу полягає в тому, що досягається зменшення густини конструкції в результаті перерозподілу матеріалу в розглянутій ділянці простору за відомих і заданих граничних умов. Результатом використання є отримання рівноміцного об’єкта в рамках розглянутої задачі.
На сьогодні SIMP-метод широко застосовується в усьому світі, а широкого застосування набув цей метод саме в адитивних технологіях (3D-друк), здатних створювати конструкції необхідної геометрії. В якості розрахункової змінної розглядається щільність матеріалу.
Основоположна частина SIMP – область проектування Ω, яка визначається за допомогою кінцевих елементів. Властивості матеріалу постійні в кожному з цих елементів і залежать від відносної щільності xi. Відносна щільність має дорівнювати 1 або 0 у розрахунковій області Ω після оптимізації. Для обмеження проміжної відносної густини використовується фактор відбраковування р. Відношення між модулем пружності та відносною густиною записується як:
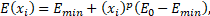
де E0 – модуль пружності матеріалу. Для чисельної стійкості Emin приймається за E0/1000, xi – відносна щільність i-го елемента; p – фактор відбраковування.
Видалення вокселів відбувається відповідно до умови найменш залученого в роботу матеріалу. Після видалення зайвого матеріалу відбувається згладжування отриманої конструкції та проводиться її КЕ аналіз (пункти 4, 5). Надалі йде оцінка оптимальності конструкції. Якщо умови мінімуму задовольняються, то отриману конструкцію розглядають як фінальну, готову до 3Д-друку і вона не потребує додаткових операцій. В іншому разі процес оптимізації повторюється (пункт 3).
Наразі топологічну оптимізацію конструкції реалізовано в таких CAD-CAE пакетах як ANSYS Discovery, Autodesk Inventor, Abaqus, TopOpt і так далі.
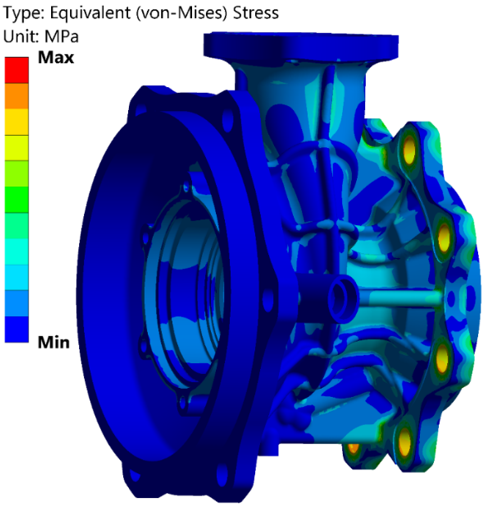
Рисунок 6 – Розрахункові напруження в конструкції
У результаті оптимізації вдалося знизити масу конструкції на 23% і при цьому коефіцієнт запасу міцності склав більше 3, що відповідає нормам міцності. Наведено порівняльну характеристику патрубків насоса окиснювача до і після оптимізації (табл. 1).
Таблиця 1 – Порівняння характеристик конструкцій

Висновки
У роботі вперше представлено результати топологічної оптимізації дослідних зразків елементів ТНА, виготовлених методом селективного лазерного сплавлення (SLM). Виявлено особливості застосування технології SLM для виготовлення силових елементів ТНА, а саме:
– досліджено можливість виготовлення складних геометричних форм, які складно або неможливо виготовити класичними способами;
– досліджено можливість багатосерійного виготовлення деталей.
Далі наведено фінальну конструкцію патрубка (рис. 4) після топологічної оптимізації. Так само виконано аналіз міцності вихідної конструкції та отриманої після оптимізації (рис. 5, 6).
У статті розглянуто процедуру топологічної оптимізації конструкцій РН на прикладі патрубка насоса окиснювача ТНА ЖРД. Представлено конструкцію патрубка окиснювача до і після оптимізації, розрахунок на міцність, оцінку його працездатності та аналіз маси конструкції. Особливу увагу приділено навантаженню внутрішнім тиском. У результаті оптимізації вдалося знизити масу конструкції на 23% і при цьому коефіцієнт запасу міцності склав більше 3, що відповідає нормам міцності. Так само важливо, що конструкція готова до використання і не потребує додаткових робіт.
Застосування топологічної оптимізації безсумнівно має великий потенціал щодо елементів ТНА та інших силових конструкцій РРД. Однак цей метод потребує ретельнішого вивчення і нарощування експериментальної бази.
Посилання
- Bendsøe M. P. Optimal shape design as a material distribution problem. Structural Optimization. 1989. Vol. 1, no. 4. P. 193–202. URL: https://doi.org/10.1007/bf01650949.
- Liu J., Ma Y. A survey of manufacturing oriented topology optimization methods. Advances in Engineering Software. 2016. Vol. 100. P. 161–175. URL: https://doi.org/10.1016/j.advengsoft.2016.07.017.
- Bendsøe M. P., Sigmund O. Topology Optimization. Berlin, Heidelberg : Springer Berlin Heidelberg, 2004. URL: https://doi.org/10.1007/978-3-662-05086-6.
- Direct Metal Laser Sintering или прямое лазерное спекание. URL: http://cantouch.ru/blog/dmls/
- Flight Control Propulsion. Flight Control Propulsion. URL: http://flightcontrolpropulsion.com.
- Bondarenko, O., Vekilov, S., Tkachov, Y., & Marchan, R. (2021). Topology optimization features of liquid-propellant rocket engine power elements manufactured by additive technologies. Journal of Rocket-Space Technology, 29(4), 106-111. https://doi.org/10.15421/452111